Strong Password-Only Authenticated Key
Exchange [*]
David P. Jablon
www.IntegritySciences.com
March 2, 1997
A new simple password exponential key exchange method (SPEKE) is described.
It belongs to an exclusive class of methods which provide authentication and key
establishment over an insecure channel using only a small password, without risk
of off-line dictionary attack. SPEKE and the closely-related Diffie-Hellman
Encrypted Key Exchange (DH-EKE) are examined in light of both known and new
attacks, along with sufficient preventive constraints. Although SPEKE and DH-EKE
are similar, the constraints are different. The class of strong password-only
methods is compared to other authentication schemes. Benefits, limitations, and
tradeoffs between efficiency and security are discussed. These methods are
important for several uses, including replacement of obsolete systems, and
building hybrid two-factor systems where independent password-only and key-based
methods can survive a single event of either key theft or password
compromise.
1 Introduction
It seems paradoxical that small passwords are important for strong
authentication. Clearly, cryptographically large passwords would be better, if
only ordinary people could remember them. Password verification over an insecure
network has been a particularly tough problem, in light of the ever-present
threat of dictionary attack. Password problems have been around so long
that many have assumed that strong remote authentication using only a small
password is impossible. In fact, it can be done.
Since the early 1990's, an increased focus on the problem has yielded a few
novel solutions, specially designed to resist to dictionary attack. In this
paper we outline the problem, and describe a new simple password exponential key
exchange, SPEKE, which performs strong authentication, over an insecure
channel, using only a small password. That a small password can accomplish this
alone goes against common wisdom. This is not your grandmother's network
login.
We compare SPEKE to the closely-related Diffie-Hellman Encrypted Key Exchange
[BM92], and
review the potential threats and countermeasures in some detail. We show that
previously-known and new attacks against both methods are thwarted when proper
constraints are applied.
These methods are broadly useful for authentication in many applications:
bootstrapping new system installations, cellular phones or other keypad systems,
diskless workstations, user-to-user applications, multi-factor password + key
systems, and for upgrading obsolete password systems. More generally, they are
needed anywhere that prolonged key storage is risky or impractical, and where
the communication channel may be insecure.
Readers who are thoroughly familiar with the work on Encrypted Key Exchange
and related Diffie-Hellman (DH) authentication methods may want to jump directly
to § 3.1 and § 4.3 to find new
results.
The rest of § 1
defines the remote password problem, § 2 defines what we
want from a solution, and § 3 describes the
specific SPEKE and DH-EKE methods. Both are reviewed in light of all known
classes of attack in §
4, and § 5
contains a fully-constrained description of SPEKE. § 6 discusses some
limitations and possibilities for these methods. § 7 shows related
efforts, and § 8
shows several uses for these methods.
1.1 The remote password
problem
Ordinary people seem to have a fundamental inability to remember anything
larger than a small secret. Yet most methods of remote secret-based
authentication presume the secret to be large. We really want to use an easily
memorized small secret password, and not be vulnerable to dictionary
attack. In this paper, we make a clear distinction between passwords and keys:
Passwords must be memorized, and are thus small, while keys can be recorded, and
can be much larger. The problem is that most methods need keys that are too
large to be easily remembered.
User-selected passwords are often confined to a very small, easily searchable
space, and attempts to increase the size of the space just makes them hard to
remember. Bank-card PIN codes use only 4-digits (about 13 bits) to remove even
the temptation to write them down. A ten-digit phone number has about 30
bits, which compels many people to record them. Meanwhile, strong symmetric keys
need 60 bits or more, and nobody talks about memorizing public-keys. It is also
fair to assume that a memorizable password belongs to a brute-force searchable
space. With ever-increasing computer power, there is a growing gap between the
size of the smallest safe key and the size of the largest easily remembered
password.
Unfortunately, most commonly-known remote password methods require a large
password. To counter the threat of attack, we assign the user painfully large
passwords, we force frequent password changes, and we issue guilt-instilling
mandates to never write the password down. It's almost as if there's an
unspoken, cavalier attitude toward the "problem users", that goes something like
this: "If they can't remember a large-enough password, then they'll get what
they deserve." This is wrong. A more enlightened attitude is needed. We must
protect our weak-willed, weak-minded users from themselves.
The problem is compounded by the need to memorize multiple passwords for
different purposes. One example of a small-password-space attack is the
verifiable plain-text dictionary attack against Kerberos login, described in [BM91], [GLNS93]. Kerberos
is by no means alone with this weakness. A general failure of many obsolete
password methods is due to presuming passwords to be large. Here's a simple
example of a bad way for Alice to verify that Bob knows a small password, S:
Alice sends a random nonce R to Bob, and Bob returns Q = h(R, S), a
one-way hash of the nonce combined with the password. This proves that he knows
S. But because the space is searchable with brute force, an eavesdropper can
perform a dictionary attack by repeatedly computing h(R,
Si) for each candidate password Si and
comparing the result to Q.
To summarize, we assume that any password belongs to a
cryptographically-small space, which is also brute-force searchable with a
modest effort. Large passwords are arguably weaker since they can't be
memorized.
So why do we bother with passwords? A pragmatic reason is that they are less
expensive and more convenient than smart-cards and other alternatives. A
stronger reason is that, in a well-designed and managed system, passwords are
more resistant to theft than persistent stored keys or carry-around tokens. More
generally, passwords represent something you know, one of the "big three"
categories of factors in authentication.
2 Characteristics of strong
password-only methods
We now define exactly what we mean by strong password-only remote
authentication. We first list the desired characteristics for these methods,
focusing on the case of user-to-host authentication. Both SPEKE and DH-EKE have
these distinguishing characteristics.
1. Prevent off-line dictionary attack on small passwords.
2. Survive on-line dictionary attack.
3. Provide mutual authentication.
4.
Integrated key exchange.
5. User needs no persistent
recorded (5a) secret data, or (5b) sensitive host-specific data.
Since we assume that all passwords are vulnerable to dictionary attack, given
the opportunity, we need to remove the opportunities. On-line dictionary
attacks can be easily detected, and thwarted, by counting access failures.
But off-line dictionary attack presents a more complex threat. These
attacks can be made by someone posing as a legitimate party to gather
information, or by one who monitors the messages between two parties during a
legitimate valid exchange. Even tiny amounts of information "leaked" during an
exchange can be exploited. The method must be immune to such off-line attack,
even for tiny passwords. This is where SPEKE and DH-EKE excel.
Mutual authentication is desirable. These methods must prove to each
of two parties that the other knows the password.
At the same time, we generate a session key for securing a subsequent
authenticated session between the parties using the password. The desirability
for integrated key exchange in authentication is discussed in [vOW96]. The basic
idea is that separating the steps of authentication and key exchange creates
opportunities for an attacker in the middle. Strong key exchange requires the
participation of both parties, and should be an integral part of the
process.
The characteristic of no persistent recorded data means the user needs
no additional symmetric, public, or private keys. There are many ways to create
a secure channel over which a clear-text password or a simple hashed-password
exchange can be sent. Our goal, however, is more ambitious: We seek a
password-only method, to make the password an independent factor,
and simplify the user's side of the system. Persistent data would have to be
generated, distributed, and securely stored, which poses additional problems.
Secret data must never be revealed, and non-secret sensitive data must be kept
tamper-proof. Either may require specially protected memory, and it weakens the
security model by adding another point of failure. Systems where the security of
a password depends on a stored key are easily constructed, but they just move
the basis of security from the password to the key. If the key is stolen, the
password can be compromised. Eliminating persistent user-keys removes this
problem, and removes the need for secure storage, enabling some special
applications, as discussed in § 8.
Both SPEKE and DH-EKE meet all of these goals, and have other desirable
characteristics which are discussed in the subsequent analysis. In § 7 we briefly
describe some other attempts to find a strong password-only method.
3 Two strong password-only
methods
The two methods of strong password-only authentication described here are
both based on a Diffie-Hellman key exchange [DH79]. A classic DH
exchange permits two parties with no prior agreement to establish a shared
secret session key. For reference, the classic DH exchange is shown in Appendix A.
DH by itself does not provide authentication, and is vulnerable to a
man-in-the-middle attack.
The SPEKE and DH-EKE methods are both forms of authenticated key
exchange. The use of DH protects the password from off-line dictionary attack,
while the use of the password in each method prevents the standard DH
man-in-the-middle attack, as discussed in § 4.3. From another
viewpoint, [BM92]
describes how the exchange amplifies the power of the shared secret
password to establish a much larger session key. Two parties, who share only a
small password (S), authenticate each other over an insecure network, proving to
each other their knowledge of S and generating a new large session key (K).
These methods use arithmetic in a huge finite group. Several such groups can
be used in DH, but for simplicity we'll limit discussion to
Zp*, where p is a huge prime. Appendix A
also contains a brief review of relevant group theory terminology and concepts
for reference. In order to fully appreciate the methods and the potential
threats against them, some knowledge of the underlying mathematics is
helpful.
In our discussion, we presume that Alice and Bob are two
well-behaved legitimate parties. In user-to-host situations, Alice is the user.
We also use the following symbols:
| S |
a small shared password for Alice and Bob. |
| p |
a huge prime number suitable for Diffie-Hellman. |
| q |
a large prime factor of p-1. |
| g |
a suitable DH base, either primitive, or of large prime
order. |
| Gx |
a subgroup of Zp* of order
x. x is a factor of p-1. |
| f(S) |
a function that converts S into a suitable DH base.
|
| RA, RB |
random numbers chosen by Alice, and Bob. |
| QA, QB |
exponential values sent by Alice, and Bob. |
| Ek(m) |
a symmetric encryption function of m using key
k. |
| h(m) |
a strong one-way hash function of m. |
| A®B: m |
Alice sends m to Bob. |
| K |
generated session key. |
3.1 SPEKE
The simple password exponential key exchange (SPEKE) has two stages. The
first stage uses a DH exchange to establish a shared key K, but instead of the
commonly used fixed primitive base g, a function f converts the password
S into a base for exponentiation. The rest of the first stage is pure
Diffie-Hellman, where Alice and Bob start out by choosing two random numbers
RA and RB:
| S1. |
Alice computes: |
QA = f(S)RA
mod p, |
A®B: QA. |
| S2. |
Bob computes: |
QB = f(S)RB
mod p, |
B®A: QB. |
| S3. |
Alice computes: |
K = h( QBRA
mod p ) |
|
| S4. |
Bob computes: |
K = h( QARB
mod p ) |
|
In the second stage of SPEKE, both Alice and Bob confirm each other's
knowledge of K before proceeding to use it as a session key. One way is:
| S5. |
Alice chooses random CA, |
A®B: EK(CA).
|
|
| S6. |
Bob chooses random CB, |
B®A: EK(CB,
CA). |
|
| S7. |
Alice verifies that CA is correct, |
A®B: EK(CB).
|
|
| S8. |
Bob verifies that CB is correct. |
|
|
To prevent discrete log computations, which can result in the attacks
described in §
4.1, the value of p-1 must have a large prime factor q.
The function f is chosen in SPEKE to create a base of large prime
order. This is different than the commonly used primitive base for DH, and its
practical importance will be discussed in § 4.2.2. The use
of a prime-order group may also be of theoretical importance.
Other variations of the verification stage are possible. This stage is
identical to that of the verification stage of DH-EKE [BM92], and
variations such as those described in [STW95] using
QB instead of the random numbers Cx in an minimal
three-message refinement apply to SPEKE as well as to DH-EKE. More generally,
verification of K can use any classical method, since K is cryptographically
large. This example repeatedly uses a one-way hash function:
| S5. |
Alice sends proof of K: |
A®B: h(h(K)) |
|
| S6. |
Bob verifies h(h(K)) is correct, |
B®A: h(K) |
|
| S7. |
Alice verifies h(K)) is correct. |
|
|
This approach uses K in place of explicit random nonces, which is possible
since K was built with random information from both sides.
3.2 DH-EKE
DH-EKE (Diffie-Hellman Encrypted Key Exchange) is the simplest of a
number of methods described in [BM92]. The method
can also be divided into two stages. The first stage uses a DH exchange to
establish a shared key K, where one or both parties encrypts the exponential
using the password S. With knowledge of S, they can each decrypt the other's
message using ES-1 and compute the same key K.
| D1. |
Alice computes: |
QA = gRA mod p, |
A®B: ES(QA).
|
| D2. |
Bob computes: |
QB = gRB mod p, |
B®A: ES(QB).
|
| D3. |
Alice computes: |
K = h( QBRA
mod p ) |
|
| D4. |
Bob computes: |
K = h( QARB
mod p ) |
|
It is widely suggested in the literature [BM92], [STW95], [Sch96 pp. 518-522]
that at least one of the encryption steps can be omitted, but this may leave the
method open to various types of attacks as described in § 4.3 and § 4.4.
The values of p and g, and the symmetric encryption function ES
must be chosen carefully to preserve the security of DH-EKE, as is discussed in
detail in § 4.
In the second stage of DH-EKE, both Alice and Bob confirm each other's
knowledge of K before proceeding to use it as a session key. However, with
DH-EKE the order of the verification messages can also be significant, as is
discussed in §
4.4.
4 Analysis of SPEKE and
DH-EKE
In the original paper on EKE [BM92], there is
some analysis of DH-EKE. Further work and refinement of EKE is presented in [STW95]. [Jas96] provides
further details on a required constraint in the proper selection of the modulus
p. [vOW96]
describes a refinement in computing discrete-logs, and discusses the selection
of the parameters for general DH-based authentication, especially with regard to
using short exponents. Results from these papers that are relevant to SPEKE are
summarized here, along with new observations about DH-EKE. A quick summary of
the threats and relevant constraints for both methods is presented in Table 4.
| Constraint |
Prevents Attack by: |
Reference |
Applies to |
| modulus p is huge |
discrete log attack |
[BM92], § 4.1 |
D S † |
| test Qx != 0, when un-encrypted |
forcing K=0 |
[BM92] |
D S |
| p-1 has large prime factor q |
Pohlig-Hellman log computation |
[BM92] |
D S |
| encrypted Qx randomly padded. |
leakage from ES(Qx) |
[BM92] |
D |
| base is primitive root of p |
partition attack on ES(Qx) |
[BM92], § 4.2.1 |
D |
| base is a generator of q |
partition attack on Qx |
§ 4.2.2 |
S |
| base = Sx mod p |
password-in-exponent attack |
§ 4.12 |
S |
| first receiver of verification of K must encrypt
Qx |
finding password S using chosen Rx,
Qx, EK(x) and password dictionary |
[STW95], § 4.4 |
D |
| use one-way hash of K |
narrowing attacks |
[STW95] |
D S |
| high bits of p must be 1 |
partition attack on EK(Qx) |
[Jas96] |
D |
| Receiver of clear Qx abort if K is small
order. or Encrypt QA, QB. |
subgroup confinement of K |
§ 4.3 |
D |
| Abort if K has small order |
subgroup confinement of K |
§ 4.3 |
S |
† D: required for DH-EKE
S: required for SPEKE
Table 4 Constraints for SPEKE and DH-EKE
In a Diffie-Hellman exchange, the use of a safe prime modulus p (where
p = 2q + 1, with prime q) and a base g which is a primitive root of p is
commonly recommended to prevent discrete log attacks. These are sufficient, but
more-than-necessary constraints. The literature [PH78, McC90] discusses
proper selection of g and p, in particular to address the concern that easier
solutions to the discrete logarithm problem make it easier to attack DH. Values
for g in DH that are generators of a huge subgroup in
Zp* are generally at least as strong as primitive
roots. However, widely available literature, with the recent exception of [vOW96], does not
discuss how the structure of Zp* is particularly
relevant to authentication systems that use DH. We address this issue in our
discussion.
We discuss three classes of attack directly related to the arithmetic used in
the DH exchange in the following sections:
| §
4.1 |
Discrete log computation. |
| §
4.2 |
Leaking information. |
| §
4.3 |
Small subgroup confinement. |
The discrete log computation inverts an exponentiation modulo p, to
reveal the exponent, and ultimately the password. The difficulty of this
computation depends on the size and character of p. The security of these
methods relies on the computation being practically impossible.
We are also concerned that the exchanged, possibly encrypted, exponentials do
not leak information about the password S. Leaking even a single bit of
information about S during a single run can be devastating, if the bit is used
to partition a password dictionary into possible and impossible candidates. [BM92] This type of
slow-leak partition attack can reduce a good-sized dictionary to a single
password candidate in a small number of runs.
Third, an attacker who knows the structure of
Zp* may be able to force the value of K to be
confined to a small subgroup, which allows a (previously overlooked) guessing or
brute force attack on K. In their security analysis of DH-EKE, [STW95] apparently
assume that K is always randomly distributed in
Zp*. This assumption is false, since the first
exponentiation of g with a random number confines the result to a smaller
subgroup at least half the time. We discuss such subgroup confinement
attacks in §
4.3.
All of these attacks are stopped with the proper constraints. § 4.5 and § 4.6 discuss
tradeoffs that can be made with speed vs. security, by using a shorter modulus.
More research is needed to increase the efficiency of these methods in light of
basic attacks. §
4.7 discusses how short exponents can safely increase speed.
In addition to Alice and Bob, we introduce some other characters who make
things interesting:
Mallory, who sits "in the middle" and intercepts, modifies, and
re-sends messages,
Eve, who listens-in on the channel and reads all exchanged messages,
and
Abby and Barry, who don't know the password, but who try to
pose as Alice and Bob.
4.1 Discrete log attack
As the security of these schemes rests primarily on exponentiation being a
one-way function, there is a general threat of an attacker computing the
discrete logarithms on the exponentials. Known methods of discrete log require a
massive pre-computation for each specific modulus.
Modulus size is a primary concern. No method is currently known that could
ever compute the discrete log for a safe modulus greater than a couple thousand
bits, however a concerted attack on a 512 bit modulus may be soon feasible with
considerable expense. Somewhere in between is an ideal size balancing speed
against the need for security, in a given application.
Furthermore, a carefully chosen prime modulus p is required to prevent easy
shortcut solutions to the discrete log problem. When p-1 has a large prime
factor q, it resists the Pohlig-Hellman discrete log attack described in [PH78]. A safe prime
of the form p = 2q+1, is one accepted way to prevent such short-cuts. A recent
analysis and survey of these issues can be found in [vOW96].
It is noted in [BM92] that if we
assume that a discrete log pre-computation has been made for the modulus, a
password attack must also compute the specific log for each entry in the
password dictionary (until a match is found). It is also noted in [BM92] that for any
session established with a modulus vulnerable to log attack, perfect forward
secrecy is no longer guaranteed (§ 4.9), providing
another reason for keeping the discrete log computation out of reach. The
feasibility of a pre-computed log table remains a primary concern, and the
efficiency of the second phase of the attack is secondary.
4.2 Leaking information
If one is not careful, the exchanged messages Qx may reveal
discernible structure, and can "leak" information about S, enabling a partition
attack. This section shows how to prevent these attacks.
4.2.1 DH-EKE partition
attack
In DH-EKE, Alice and Bob use a Diffie-Hellman exponential key exchange in the
group Zp*, with a huge prime p, where p-1 has a
huge prime factor q. [BM92] use the
traditional preference for g as a primitive root of p. In fact, g must be
primitive to prevent a partition attack by an observer [Bel96]. A third
party can do trial decryptions of ES(gRX
mod p) using a dictionary of Si. If g is not primitive, a bad
guess Si is confirmed by a primitive result. In general, the
encrypted exponentials Qx must contain no predictable
structure to prevent this attack against DH-EKE. Constraining g to be primitive
insures a random distribution across Zp*.
g must be primitive
The properties of the encryption method itself may also be a concern,
although the primary concern is that the clear-text be random, which simplifies
the constraints on the function ES. Toward this goal, other
recommended constraints for DH-EKE are:
p must be slightly less than a power of 2. ([Jas96] describes
how much less.)
padding bits to fill to the block-size of ES must be random.
SPEKE does not require these constraints, since it does not use symmetric
encryption.
4.2.2 SPEKE partition
attack
Using a primitive base is not required in SPEKE. If the base f(S) is
an arbitrary member of Zp*, since the exponentials
are not encrypted, an observer can test the result for membership in smaller
subgroups. When the result is a primitive root of p, he knows that the base also
is primitive. For a safe prime p, this case reveals 1 bit of information about
S. When p varies, as has been recommended when using a reduced modulus size (§ 4.6, § 4.7), new
information from runs with different p allow a partition attack to reduce a
dictionary of possible Si.
When, for any S, the base f(S) is a generator of a particular large
prime subgroup, then no information is leaked through the exponential result.
Suitable functions for f(S) create a result of known large order. One
example is shown in § 4.13. One
important limitation on f is discussed in § 4.12. We assume
the use of a large prime-order base in SPEKE for the rest of the discussion.
Because SPEKE does not encrypt the exponentials, a formal analysis of
security may be simpler to achieve for SPEKE than for DH-EKE. The prime-order
subgroup is the same as that used in the DSA and Schnorr digital signature
methods.
4.3 Subgroup confinement
In a subgroup confinement attack on a Diffie-Hellman exchange, the goal is to
confine K to a predictable and small set of values, by causing one or both
parties to use a number of a small order t as the base of exponentiation.
Use of a safe-prime p = 2q+1 reduces, but does not eliminate the presence of
small subgroups, as shown in figure 4.3.
Even with a safe-prime p, Zp* still has the small
subgroup G2. We'll show two versions of the attack.
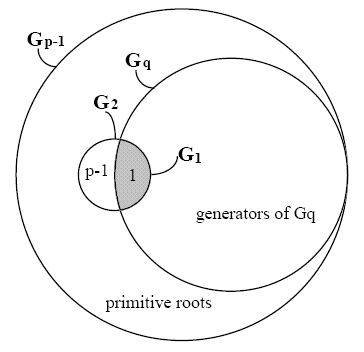
Figure 4.3 Subgroups of Zp* for a safe
prime p = 2q+1
In the man-in-the-middle version of this attack described in [vOW96], both
parties are unaware that Mallory has intercepted and modified the exponentials.
Knowing that t is a small prime factor of p-1, Mallory intercepts both
QA and QB and sends QA(p-1)/t to Bob
and QB(p-1)/t to Alice. This converts the exponentials
into generators of the small subgroup Gt. [1]
Both Alice and Bob go on to compute a shared value for
K, which is confined to Gt. Mallory then has the easy job of
finding K with a brute force attack. [vOW96] recommends
the use of a large prime order subgroup to thwart this attack, making
confinement to the only small subgroup G1 trivial to detect.
An alternate safeguard when the factorization of p-1 is known is to test K for
membership in all small subgroups, and abort if it is confined.
We show that a confinement attack also occurs when Barry masquerades as Bob,
and sends a value QB of small order t directly to the other. This is
feasible in SPEKE, or in DH-EKE when QB is unencrypted. This one-side
attack also results in K being confined to Gt, which gives
Barry a 1/t chance of guessing K. He may get lucky with a tiny t. The middle
attack is only a threat for SPEKE, since it requires that both QA and
QB be sent unencrypted.
One path to a solution is to try to eliminate small subgroups in
Zp*. The closest we can come to this is to select p
as a safe prime, which yields the small subgroups G2 and
G1. An easy solution for SPEKE is to test the value of K. In
this case, insuring that K is a member of G2 prevents the
attack. Each side tests K and only proceeds if 1 < K < p-1, since
G2 = {1, p-1}. For DH-EKE, another solution is to always
encrypt both exponentials so that an attacker on either side cannot (feasibly)
cause Qx to be of small order.
Another approach to avoiding confinement in SPEKE is to test K for membership
in all subgroups other than Gq, where q is a large prime, and
f(S) is of order q. If K is found to be a member of any group other than
Gq, then the protocol must be aborted. This is conveniently
done if each receiving party raises Qx to the power (p-1)/q
before computing K. This forces K to be a member of Gq, so
that testing to insure K does not equal 1 prevents any confinement. [2]
If Qx is a member of Gq, then
this extra exponentiation is just a one-to-one mapping that shuffles K to
somewhere else in the group. The extra exponentiation adds negligible cost,
since it can be performed as multiplication in the exponent.
4.4 Omitting encryption in
DH-EKE
[STW95] shows
that when the party who first receives verification of K from the other omits
the step of encrypting the exponential, then DH-EKE is open to a dictionary
attack on the password. [BM92] describes
this attack as it applies to other public-key variants of EKE. In this
description, presume that an attacker Abby is posing as Alice, and that the step
of encrypting QA is omitted.
| D1. |
Abby computes: |
QA = gRA mod p, |
A®B: QA |
| D2. |
Bob computes: |
QB = gRB mod p, |
B®A: ES(QB)
|
| D3. |
Abby yawns. |
|
|
| D4. |
Bob computes: |
K = h( QARB
mod p ) |
|
| D5. |
Alice computes: |
Abby chooses a random V, |
A®B: V |
| D6. |
Bob computes: |
Bob chooses a random CB, |
B®A: EK(CB,
EK-1(V))) |
| D7. |
Abby leaves the building. |
|
|
In this case, Abby has temporarily displaced Alice, and it may appear to Bob
as an ordinary communication failure. At this point Abby performs the off-line
attack:
For each Si,
Decrypt ES(QB) with candidate password
Si to obtain candidate QB'.
Compute K' = QB' RA.
Decrypt V with K' to get CA'.
Decrypt EK(CB,
EK-1(V))) with K' to get (XB, XA).
If XA equals CA',
Abby knows that Si = S.
The problem is due to the fact that the protocol makes Bob show his knowledge
of K before Abby shows hers. This attack will not succeed if the order of
verification is changed so that the first to receive proof is not the same party
as the sender of the unencrypted exponential.
Encryption is a delicate issue in DH-EKE. Omitting one of the encryptions in
DH-EKE raises the possibility of either this protocol attack, or the one-sided
small subgroup confinement attack described in § 4.3. On the other
hand, the presence of encryption poses the threat of the partition attack
that must be dealt with carefully as described in § 4.2.1.
The protocol attack described here is not possible in SPEKE. In SPEKE rather
than encrypting Qx with the password, the password is hidden
on each side by raising it to a random exponent. In order to compute K given
QA and QB, one must either derive the value of
RB from QB or derive RA from QA.
This requires a discrete log computation.
4.5 Using a short modulus
To increase the speed of exponentiation, the modulus size can be reduced. But
since the huge size of the modulus is a cornerstone of DH security, we must be
extremely careful here. If the modulus size is reduced well below, say, 600
bits, the threat of discrete log attack becomes significant. [BM92] argues both
for and against a decreased modulus. We summarize the debate here.
Pro: A decreased modulus size makes the method faster.
Con: A decreased modulus size permits feasible (though expensive)
discrete log attack.
Con: Also, for a session established with a modulus vulnerable to log
attack, perfect forward secrecy is no longer guaranteed (see § 4.9).
Pro: The log attack can be mitigated by a user-specific or
frequently-changing modulus. This is a disincentive for a third-party attacker
to spend much time or money computing a discrete log for a particular number.
In order to synchronize a variable modulus for both parties, it has been
suggested that one party choose the parameters for the other [BM92,
Jas96]. This raises new issues of trust. We must now ask whether an
attacking party could maliciously choose parameters so as to gain information
about the password from the other, or to make it easier to obtain a key without
using the proper password.
4.6 Uncertified ephemeral
parameters
We continue the debate, which is now in terms of whether or not one party
should choose the ephemeral DH parameters. Presume that Bob chooses p and g
randomly from a pre-computed set, and sends them to Alice prior to the exchange.
As we maintain our goal of not requiring persistent public keys, these
parameters must be uncertified. So, how can Alice trust them?
Con: Barry masquerading as Bob can deliberately send Alice a non-prime
or non-safe prime modulus and/or a base with properties that aid in a partition
attack against Alice's password (as described in § 4.2).
Pro: Alice can use primality and other tests to insure that the
parameters are safe. [BM92]
Con: Practical tests for primality are probabilistic, and are only
guaranteed to work for small or randomly chosen huge primes. An attacker
might be able to deliberately create a non-prime that can pass Alice's test, and
lead to an attack. (Also, [BM92] refers to a
communication with Odlyzko about a potential "trap door" modulus, without
further explanation.)
A simple way to avoid the debate is to embed fixed safe parameters in the
system, where the modulus is large enough to "permanently" preclude the discrete
log attack. It has been suggested that 1000 or 2000 bits is adequate for
long-term security. The use of a short exponent as is discussed next may make
this practical for many situations.
| Constraint |
Reason |
Reference |
Applies to |
| Test that p is prime |
non-prime p with calculated log |
[BM92] |
D S |
| Test that q is a large prime |
non-safe prime p with calculated log |
[BM92] |
D S |
| Certified parameters |
p has hidden trap door (?) |
[BM92] |
D S |
| Certified parameters |
chosen false-prime p or q |
§ 4.6 |
D S |
Table 4.6 Special constraints for chosen parameters
If we continue the debate in search of a safe way to use a smaller modulus,
the analysis becomes more complex. To end our discussion on a positive note, we
ask whether there may be some perfect test that Alice can efficiently perform to
guarantee that the parameters are trusted to not leak information in the first
stage, at least until Bob proves who he is. Toward this goal we note that SPEKE
can operate in a large prime subgroup of order q << p, and that perfect
primality tests for non-huge q are possible.
It may also be interesting to consider the case where p and q are also kept
secret, possibly within a tamper-proof hand-held device. Though this violates
our characteristic 5, it might be useful if the modulus size must be imprudently
small. Considering a normal SPEKE exchange with p, q, and S kept secret may also
be of interest.
4.6.1 A user-to-station
protocol
If despite the warnings in the preceding section, we still desire to let Bob
choose the DH parameters for Alice, we may want to omit our desired
characteristic 5b of §
2. Bob can sign the parameters with his private key, and require all users
to have a certified copy of his public key to verify the signature. Note that
this may impose less of a key management problem than the dual-signature
approach used in the Station-to-Station protocol [DvOW92] (also see
§ 7). If Bob is a
relatively secure site compared to Alice, his key may change only rarely.
Further, if parameter generation is performed by a trusted authority at a secure
central site, we might embed a public key of the trusted authority in read-only
memory within all parties' systems. The trusted authority would periodically
send out lists of certified safe parameters.
4.7 Using a short exponent
A less radical approach to increasing speed is to decrease the exponent size
to be merely large, leaving the modulus huge. [vOW96] discusses
this in detail. The number of bits in the exponents must be at least double the
number of bits (t) that are required for K, but this is typically much less than
the number of bits in p.
Their conclusions suggest two safe approaches, where the exponents can be
reduced to size 2t bits:
1. Use a huge safe prime modulus p with a primitive base of 2, or better yet,
a prime-order base of 2.
2. Use a huge prime modulus p with a base of large
prime order q, where q has at least 2t bits.
The first approach works with either DH-EKE or SPEKE, although DH-EKE needs
further protection from the small-subgroup confinement attack. Using a base g =
2 further increases the speed. When g = 2, note that the two methods cannot use
the same safe primes. A safe prime p suitable for DH-EKE must have 2 be a
primitive root of p (see § 4.2.1), while a
safe prime p suitable for SPEKE should ideally have 2 be of order q.
The use of a large prime subgroup where q << p has the advantage of
speeding up the generation of the DH parameters. This works with SPEKE, but it
cannot be used with DH-EKE which requires a primitive base.
4.8 More desirable
characteristics
In [DvOW92]
the security of general authenticated key exchanges is discussed, and several
desirable protocol characteristics are described. We start numbering these at 6
to add to the five characteristics listed in § 2.
6. Perfect forward secrecy
7. Direct
authentication
8. No timestamps
9.
Hidden identity.
Perfect forward secrecy means that disclosure of the password doesn't
reveal prior recorded conversations. Direct authentication means that
both sides verify the session key before proceeding. No timestamps means
that the messages do not contain time-dependent data, which might require time
synchronization between the parties. Without further discussion, we note that
both DH-EKE and SPEKE meet the first three objectives.
Only the ninth characteristic, hidden identity is problematic. Neither
of the methods described here hides the identity of the user from a passive
observer. This limitation could be overcome with an additional prior standard DH
exchange that establishes an unauthenticated key, to encrypt the user's
identity. A man-in-the-middle attack would reveal this hidden identity, perhaps
at the expense of being detected. We also note that while the somewhat-related
Station-to-Station protocol (§ 7) can hide identity from passive attack, it also
reveals identity to a man-in-the-middle at the expense of disrupting the
run.
The problem of authenticating with a perfectly-hidden identity seems to be
intractable without using a previously established secure session or large
public keys. In these methods, the problem is related to the fact that the
secret is shared. In order to choose the appropriate secret for a particular
party, one needs to know the identity of the party prior to the exchange.
However, prior to the exchange we assume that no secure channel exists over
which to send the identity. We forgo any further analysis of this
chicken-and-egg problem.
These characteristics have been covered in the referenced literature, with
respect to key exchanges in general. At least one more desirable characteristic
of these password methods is revealed as we consider the next attack.
4.9 Stolen session key
attack
In an analysis of several flavors of EKE, [STW95] describes a
variation of what they refer to as the Denning-Sacco Attack, where a
stolen session key K is used to mount a dictionary attack on the password. The
attack on the public-key flavor of EKE is also noted in [GLNS93]. [STW95] correctly
points out that DH-EKE resists this attack (as does SPEKE). Resistance to this
attack is closely related to perfect forward secrecy, which also isolates one
kind of sensitive data from threats to another.
We note that, in DH-EKE, a stolen value of RA in addition to K
permits a dictionary attack against the password S. For each trial password
Si, the attacker computes:
K' =
(ESi-1(ES(gRB)))RA
When K' equals K, he knows that Si equals S. SPEKE is also
vulnerable to an attack using RA to find S. These concerns highlight
the need to promptly destroy ephemeral sensitive data, such as RA and
RB.
[STW95] also
notes a threat when the long-term session key K is used in an extra stage of
authentication of the extended A-EKE method [BM94, and § 7], a dictionary
attack is possible using the extra messages. To counter this threat, one can use
K for the extra stage, set K' = h(K) using a strong one-way function, and
promptly discard K.
4.10 Verification stage
attacks
The verification stage of either DH-EKE or SPEKE is where both parties prove
to each other knowledge of the shared key K. Because K is cryptographically
large, the second stage is presumed to be immune to brute-force attack, and thus
verifying K can be done by traditional means. However, the order of verification
may be important to resist the protocol attack against DH-EKE as was discussed
in § 4.4.
4.11 Detecting on-line
attack
The threat of repetitive on-line guessing by a masquerading user can be
mitigated by a careful logging and accounting of invalid access attempts. The
idea is to limit the number of illegal access attempts against any single
password, and require that the password be changed before the threshold is
exceeded. The threshold should be based on the known (or suspected) size of the
password space. It is also advantageous to keep separate per-password and total
system counts of invalid attempts to detect both attacks on a single account,
and broad-scale attacks that do not exceed any single user's threshold.
It may be tempting to try to distinguish between accidental mistakes and
illegal attempts, by noting that most mistakes are followed immediately by a
valid access. However, a clever attacker may be able to anticipate or delay a
legitimate run, and perform a few quick guesses against the same account before
letting the legitimate run succeed. Thus, even apparently accidental mistakes
should be counted, by both parties, and viewed with suspicion.
The case of a masquerading host is a little different. Whereas the host
usually has long-term storage for logging errors, the user's system may not. It
is generally foolish to rely completely on the user himself to enforce security
policy dealing with suspicious bad attempts. The user's system should at least
keep a short-term count of bad attempts and (securely) update the host with this
count the next time access is granted. The host may also alert the user of bad
access attempts at this time. These methods greatly deter guessing attacks
against both the user and the host.
4.12 The "password-in-exponent"
attack
It is generally a good idea for f(S) to create a result of the same known
order for all S, so that testing the order of the exponential doesn't reveal
information about S. When considering suitable functions, it may be tempting to
choose f(S) = gch(S) for some fixed prime-order
gc and some well-known hash function h. Unfortunately, while this is
a convenient way to convert an arbitrary number into a generator of a
prime-order group, it creates an opening for attack. [3]
To show the attack, let's assume that gc = 2, and h(S) = S, so
that f(S) = 2S. Alice's protocol can be rewritten as:
Choose a random RA.
Compute QA = 2(S RA) mod p.
Send QA to Bob.
Receive
QB from Bob.
Compute K =
QBRA mod p.
Bob should perform his part, sending QB to Alice. The problem is
that an attacker Barry can perform a dictionary attack off-line after performing
a single failed exchange. His initial steps are:
Choose a random X.
Compute
QB = 2X.
Receive QA from
Alice
Send QB to Alice.
Receive verification data for K from Alice.
Barry then goes off-line to perform the attack as follows:
For each candidate password S':
Compute K' =
(QBX)1/S' mod p.
Compare Alice's verification message for K to
K',
when they match he knows that S' = S.
This attack works because:
K' =
QA(X/S') mod p
= 2(S RA)(X/S') mod p
= 2(X
RA S/S') mod p
= QB(RA S/S')
mod p
=
K(S/S') mod p
Thus, when S' = S, K' = K. More generally, the attack works because the
dictionary of passwords {S1, S2, ..., Sn} is
equivalent to a dictionary of exponents E = {e1, e2, ...,
en}, such that for a given fixed generator gc, the value
of f(Si) for each candidate can be computed as
gcei. This allows the password to be
effectively removed from the DH computation.
In general, we must insure that no such dictionary E is available to an
attacker. We should note that while it is true that for any function f there
will always be some fixed gc and hypothetical dictionary E that
corresponds to f(S), for most functions f, computing the value of each
ei requires a discrete log computation. This makes the dictionary E
generally unknowable to anyone. As a specific example, for the function f(S) =
S, the attack is infeasible.
The password-in-exponent attack is possible only when f(S) is equivalent to
exponentiation (within the group) of some fixed gc to a power which is a known
function of S.
The attack is also a problem for DH-EKE, when ES(x) =
xS and ES-1(x) = x1/S. Although [BM92] doesn't
discuss this case, they describe how this class of attack affects the PK-EKE
protocol, attributing discovery of the problem to Li Gong.
4.13 Choosing f(S)
As discussed earlier, a preferred choice of f(S) in SPEKE creates a generator
of prime order. An easy way to avoid the attack in §4.12 is to use f(S) =
S(p-1)/q mod p. For safe prime p, f(S) = S2.
4.14 Application to
Kerberos
[Jas96]
applies the DH-EKE method to Kerberos authentication between a client and the
Key Distribution Center (KDC). The goal is to simultaneously solve three
long-standing limitations in the system, related to dictionary attacks,
dependence on timestamps, and password chaining. Password chaining is the
ability of an attacker to use an old password to determine a new one. The
reference describes how DH-EKE prevents this. The proposal uses a mild form for
ordinary login, and a strong form for specially protecting the password-change
protocol. The proposed protocol (PA-ENC-DH) uses only the first stage of DH-EKE,
and omits the verification of K.
By omitting verification of K, there is no direct authentication. One result
is that the KDC cannot distinguish valid from invalid access attempts; It can
only count the total number of attempts. A tradeoff is being made between the
size of the minimally secure password and the total number of allowed uses. Such
a system may be impractical for protecting very small passwords. A system that
performs direct authentication by verifying K and distinguishing valid from
invalid attempts would be friendlier. With this improvement, the frequent user
who rarely mistypes his password is not penalized with frequent demands to
change the password.
5 A fully constrained SPEKE
Despite the length of the preceding analysis and discussion, a fully
constrained SPEKE method is simple in structure. The description here presumes a
well-known safe prime p and random numbers RA and RB of
suitable size. Other formulations are possible.
Stage 1:
A®B:
QA = S(2 · RA) mod p.
B®A: QB =
S(2 · RB) mod p.
Alice:
K = QB(2 · RA) mod p.
Bob: K = QA(2 ·
RB) mod p.
Each aborts if K
< 2.
Stage 2:
B®A:
VB = h(h(h(K))).
Alice verifies VB.
A®B: VA =
h(h(K)).
Bob verifies
VA.
Both then compute the shared authenticated session key K' = h(K), and
both promptly destroy all copies of K, RA, RB and, if
possible, S.
Our constraints would not be complete without mention of the often
controversial subject of bit-lengths. Following the standard sizes used for the
DSA [NIST94],
using 512 to 1024 bits for p and 160 bits for random exponents, resulting in an
80-bit K, may be sufficient for many uses. Using 1024 bits for p and 336 bits
for the exponents has been recommended for DH-EKE in [Jas96] for
long-term safety.
6 Other limitations and
possibilities
Here are some apparent limitations of any password-only scheme, in light of
dictionary attacks:
The method must be interactive.
The password-verifier can always perform dictionary attack.
The password cannot be a private key in a public-key method.
Without an interactive method, the password verification messages can be used
in simplistic dictionary or replay attacks. Both parties must be active
participants. We further accept that anyone in a position to verify the password
can find it with brute-force. This can be done by simulating the actions of the
other party using each candidate password. This limitation is mentioned in [BM92].
Passwords as private-keys in a public-key system would be wonderful, but the
holder of the corresponding public-key is then in a position to perform
dictionary attack -- which defeats the purpose of a public-key. Further pursuit
along these lines leads into the domain of identity schemes, which are quite
complex and involve a trusted third-party. [Sch96 p. 115]
Password methods are attractive for their simplicity, convenience, and
strength. Where the password can be memorized, it need not be recorded and
possibly stolen. The attraction of key-based methods is in the richness and
power of public-key and non-interactive techniques. By carefully setting
expectations, both classes of methods can be widely promoted. Strong hybrid
systems can use independent key-based and password-only methods to complement
each other.
Need for a trusted path
One of the limitations of any password method is reflected in the need for a
trusted path. In a classical system this refers to the integrity of the
entire system from the user's fingers at a keyboard to the final destination
where the password is verified. In a network, password-only methods can be used
to "shorten" the trusted-path to end at the software on the user's local
processor. The path no longer requires a prior secure network channel. However,
any risks to the integrity of the local system are still relevant.
Formal verification
Although strong password-only methods based on Diffie-Hellman have been
studied for several years, more formal analysis of the security of SPEKE and
other methods would be valuable. Due to its simple structure, SPEKE may more
easily facilitate such analysis. The ability to use a prime-order subgroup may
also be significant in this regard.
7 Other related work
Only a few other password-only methods have been designed that successfully
address the goal of preventing off-line dictionary attacks. More complex
variations of EKE using public-key encryption are described in [BM92]. DH-EKE and
SPEKE have an advantage over these in being extensible to allow the host to
store a one-way hashed form of the password, in methods such as A-EKE [BM94]. In these
extended methods, Bob uses the one-way hashed password to verify possession of
the clear-text password by Alice. When using this type of extension, we make
Alice compute the hashed form, and use S to represent the hashed password in the
first stage of the exchange.
A few other approaches to strong password-only protocols have also been
explored, with varying degrees of success and complexity.
[GLNS93]
describes both three-party and two-party protocols based on using secret
public keys. The authors express a concern about finding a suitable
public-key method for these protocols, which require that any random number of
appropriate length be a valid public-key. The paper further describes
stored-public-key-assisted protocols, and discusses guessing attacks, Kerberos
login, the important concept of verifiable plain-text, which was originally
introduced by these authors.
[Gon95]
describes an optimal 3-message version of the two-party secret-public-key
protocol. [STW95] shows an
optimal 3-message form of DH-EKE, which applies equally well to SPEKE. [4]
Fortified Key Negotiation [Sch96 p. 522], [And94] is another
method which resists dictionary attack, at the expense of reducing the effective
size of the password space.
Other variations on the password-only theme are three-party exchanges, where
multiple shared secrets are held by a common trusted authentication server who
mediates the process of exchange between two parties. [STW95] points out
a weakness in some instances of these.
An earlier promising approach was the Shamir and Rivest Interlock Protocol,
as used by Davies and Price, of which a brief historical account appears in [Sch96 pp. 54-55].
An attack on the Interlock Protocol for authentication is described in [BM93], and a recent
attempt to patch this hole is described in [Ell96].
The Station-to-Station protocol described in [DvOW92] is
interesting for the sake of comparison, although it depends on the deployment of
private and public keys, in violation of our desired characteristic 5 (§ 2). The protocol
uses a DH exchange and encrypts the exponentials in a manner similar to DH-EKE,
but using public-key encryption.
Still further away along the spectrum of methods are identity-based schemes,
which can use zero-knowledge ideas to prove knowledge of a secret held by
another party. These do not provide an authenticated key exchange, and they do
not allow the "secret" to be cryptographically small. A brief review of these is
also included in [DvOW92].
8 Uses of password-only authenticated
exchange
With a strong password-authenticated key exchange, even small passwords can
be safely used. The host is presumed to detect and deter on-line attacks, and
the protocol itself prevents off-line attacks. These methods are ideal in some
applications for several reasons: secure key storage can be problematic,
large-key input can be cumbersome, and passwords may need to be better
protected. Several applications for strong password-only exchanges are mentioned
here.
In § 4.14 we
discussed using DH-EKE or SPEKE to correct deficiencies in Kerberos. The same
ideas can be used to upgrade many other vulnerable network login systems, which
can be essential for new uses such as personal-computer remote banking, and
general computer login over the Internet.
In systems where only a numeric keypad is available, such as cellular
telephone authentication, a secure, short numeric password is especially
convenient. TV remote-controlled set-top boxes might be another area of new
applications. These environments may also preclude long-term storage of
persistent keys.
Diskless workstations are another class of device where it is inconvenient to
have locally stored keys. Password-only methods are ideal for establishing an
initial connection to a trusted host, and to obtain the user's safely stored
credentials. This concept of remote storage of long-term credentials with a
secure download has been used in the SPX authentication system. [TA91]
Any device or system that uses these methods can be generic, in that
it is not preprogrammed to speak only for a particular user, or to speak to any
particular host. Alternative approaches using a persistent public-key need to
embed a key which designates a specific trusted authority. This can be
inconvenient. Password-only methods make it easier to deploy a system that has
no such embedded prior agreement. This model may better fit the "commodity"
market model for software and hardware devices.
The concept of bootstrapping a new secure system is broad, and is best
illustrated with a common case. You're installing a new network workstation from
a CD-ROM. Somewhere during installation you're prompted to enter a name and
password to let you join the secure corporate network. Unless some additional
site-specific keys are manually installed on the system, a strong password-only
method is needed to allow the new station to make a secure channel to the rest
of the network. Once an authenticated channel is established, the station can
automatically obtain any further credentials or keys. Similar "bootstrapping"
situations arise in almost all secure systems.
Though we've focused so far on user-to-host authentication, password-only
methods may be important for direct user-to-user authentication. [Ell96] describes
the use of an interactive series of questions and answers to authenticate the
identity of an "old friend, out of touch" across a network. The idea is to prove
to each other that they know common facts, without revealing those facts. Such
situations are actually quite common. Password-only methods solve this general
authentication paradox, which is present even in some face-to face situations.
For example, you may want to prove that your bank knows your "secret" account
numbers, and your bank wants you to prove that you know your "secret" social
security number, but neither wants to reveal the information directly to the
other. This is solved by these methods. Of course, given that much of this type
of shared information is not as secret as we'd like it to be, a series of
exchanges may be needed to prove further small amounts of shared knowledge, to
build confidence in the authentication.
Multi-factor authentication may be needed when neither a stored key nor a
memorized password is strong enough. In a hybrid system, one should strive to
make the password an independent factor, so that its security does not
depend on persistent stored keys, and vice-versa. Password-only methods can be
combined with key-based method to build systems that can tolerate either a
stolen password or a stolen key.
9 Summary
We've introduced a new password-only authentication protocol, SPEKE, which
appears to be at least as strong as the closely related DH-EKE method. Using
only a small password, these methods provide authentication and key
establishment over an insecure channel, and are immune to off-line dictionary
attack.
A review of the classes of attack against these DH-based methods includes
some new observations, and new constraints which are required to keep both
methods safe. These constraints are listed as a convenience to implementors.
Concerns raised about receiving unauthenticated DH parameters argue for the use
of either a fixed huge modulus, or certified parameters, or the need for further
research. In any case, it is practical to increase speed by using shorter
exponents.
Strong password-only methods have many uses, by themselves, or in
multi-factor authentication systems. It is apparent that password-only methods
can achieve things that no stored-key method can achieve, and vice-versa. A
well-designed system can leverage the power of small, easily-memorized
passwords, adding significant strength to the foundation for remote
security.
10 References
[And94] R. J. Anderson and T. M. A. Lomas, "Fortifying Key
Negotiation Schemes with Poorly Chosen Passwords", Electronics Letters,
v. 30, n. 13, June 23, 1994, pp. 1040-1041.
[Bel96] S. M. Bellovin, private communication.
[BM92] S. M. Bellovin and M. Merritt, "Encrypted Key
Exchange: Password-Based Protocols Secure Against Dictionary Attacks",
Proceedings of the I.E.E.E. Symposium on Research in Security and
Privacy, Oakland, May 1992.
[BM93] S. M. Bellovin and M. Merritt, "An Attack on the
Interlock Protocol When Used for Authentication", I.E.E.E. Transactions on
Information Theory , v. 40, n. 1, January 1994, pp. 273-275.
[BM94] S. M. Bellovin and M. Merritt, "Augmented Encrypted
Key Exchange: a Password-Based Protocol Secure Against Dictionary Attacks and
Password File Compromise", AT&T Bell Laboratories (c. 1994).
[DH79] W. Diffie and M. E. Hellman, "Privacy and
Authentication: An Introduction to Cryptography," Proceedings of the
I.E.E.E., vol. 67, No. 3, pp. 397-427 (Mar. 1979)
[DvOW92] W. Diffie, P.C. van Oorschot, and M. Wiener,
"Authentication and Authenticated Key Exchanges", Designs Codes and
Cryptography", 2, 107-125, (1992)
[Ell96] C. Ellison, "Establishing Identity Without
Certification Authorities", Proceedings of the Sixth Annual USENIX Security
Symposium, San Jose, July 1996, pp. 67-76.
[GLSN93] L. Gong, M. Lomas, R. Needham, & J. Saltzer,
"Protecting Poorly Chosen Secrets from Guessing Attacks", I.E.E.E. Journal on
Selected Areas in Communications, Vol. 11, No. 5, June 1993, pp. 648-656.
[Gon95] L. Gong, "Optimal Authentication Protocols
Resistant to Password Guessing Attacks", Proceedings of the 8th IEEE Computer
Security Foundations Workshop, County Kerry, Ireland, June 1995, pp. 24-29.
[Jas96] B. Jaspan, "Dual-workfactor Encrypted Key Exchange:
Efficiently Preventing Password Chaining and Dictionary Attacks", Proceedings
of the Sixth Annual USENIX Security Conference, July 1996, pp. 43-50.
[McC90] K. McCurley, "The Discrete Logarithm Problem",
Cryptology and Computational Number Theory, Proceedings of Symposia in
Applied Mathematics, vol. 42, 1990, pp. 49-74.
[NIST94] National Institute of Standards and Technology,
NIST FIPS PUB 186, "Digital Signature Standard", U.S. Department of Commerce,
May 1994.
[PH78] Pohlig & Hellman, "An Improved Algorithm for
Computing Logarithms over GF(p) and its Cryptographic Significance", I.E.E.E.
Transactions on Information Theory, pp. 106-110, January 1978.
[Sch96] B. Schneier, "Applied Cryptography Second Edition",
John Wiley & Sons, 1996.
[STW95] M. Steiner, G. Tsudik, and M. Waidner, "Refinement
and Extension of Encrypted Key Exchange", Operating Systems Review, vol.
29, Iss. 3, pp. 22-30 (July 1995).
[TA91] J. Tardo & K. Alagappan, "SPX: Global
authentication using public key certificates", Proceedings of I.E.E.E.
Computer Society Symposium on Research in Security and Privacy, Oakland, pp.
232-244, May 1991.
[vOW96] P. C. van Oorschot, M. J. Wiener, "On
Diffie-Hellman Key Agreement with Short Exponents", Proceedings of Eurocrypt
'96, Springer-Verlag, May 1996.
Appendix A Group theory relevant to
Diffie-Hellman methods
Finite groups have interesting properties that are used in Diffie-Hellman and
the SPEKE and DH-EKE methods discussed in this paper. Several finite groups can
be used in DH, but for simplicity we limit discussion to
Zp*, the group of integers from 1 to p-1, under
multiplication modulo p, where p is a huge prime. Exponentiation modulo p is a
one-way function, for suitable p, due to the difficulty of computing discrete
logarithms.
Zp* is also known as the multiplicative group of
the Galois field of integers modulo p, or GF(p)*. When showing
arithmetic within these groups, it is traditional to sometimes omit "mod p". As
in any group, for any x and y which are members of
Zp*, the product of x and y is also a member, and
thus exponentiation always remains within the group. In other words:
For each x which is a divisor of p-1, the group
Zp* contains a subgroup Gx
of order x, that is, Gx contains x elements.
Zp* = Gp-1. Every group
Gx contains the trivial subgroup G1,
consisting of {1}, and the subgroup Gx itself. A group
Gq of prime order q has no subgroups other than
Gq and G1. A generator
g of Gx is a number such that the set {g1,
g2, ... , gx} includes all elements of
Gx. A generator of Gp-1 is said to be a
primitive root of p. A number is said to be of order x when it is
a generator of Gx. If g is of order x, then gx is
congruent to 1 mod p.
Also note that arithmetic within the exponent must be done modulo p-1.
- For any x,y: xy is congruent to
xy mod (p-1) mod p.
This is seen from
Fermat's Theorem:
- Given a prime p, for every a such that gcd(a,
p) = 1, ap-1 mod p = 1.
The
traditional DH exchange uses two random numbers RA, and RB
to negotiate a shared key K:
Alice®Bob:
QA = gRA mod p
Bob®Alice:
QB = gRB mod p
Alice computes: K = QBRA
mod p
Bob computes:
K = QARB mod p
A prime where p-1 has only small factors is called smooth.
Smooth primes are avoided in these methods because they allow a much faster
discrete log computation [PH78], ruining
exponentiation as a useful one-way function. It is easy to select a non-smooth
prime by insuring that p-1 has a large prime factor q. Using a safe-prime
of the form p = 2q+1, where q is prime, and where the base g is a primitive root
of p, is commonly recommended in DH. However, other choices are sometimes
preferable. [vOW96] recommends
using g as a base of order q to force all results within the large prime
subgroup Gq.
Note that a safe prime is somewhat different from strong primes, which
refers to a more complex (and debatable) set of constraints for the prime
factors of a number n = pq, in methods such as RSA.
Footnotes
[1]
Let y
= x(p-1)/t for an arbitrary x. Since yt =
(x(p-1)/t)t is congruent to 1 mod p, it can be seen that
the order of y is a factor of t. Since t is prime, y is either of order t or of
order 1.
[2] From
footnote 1 in § 4.3, we know Qx is a member of Gq.
Consider any Gt and Gq, q is prime, and t < q.
We can see that the intersection of Gt and Gq =
G1. Since K is a member of Gq, if K is also confined to
Gt, then K is a member of G1, or K = 1.
[3] This
attack was not noted in the Oct. '96 ACM CCR version of this paper. The problem
was found independently by at least myself, Li Gong, and Susan Langford.
[4]
Whether a minimal message protocol is truly "optimal" depends on the desired
goal, and on the cost and speed of communication vs. computation. For example,
optimizing SPEKE for minimal time to completion may require more than three
messages to maximize parallel processing of both parties.
[*] An
earlier version of this paper appeared in ACM Computer Communication Review,
vol. 26, no. 5, Oct. 1996.
Contents
- Introduction
1.1 The
Remote Password Problem
- Characteristics of
strong password-only methods
- Two strong
password-only methods
3.1 SPEKE
3.2 DH-EKE
- Analysis of SPEKE and
DH-EKE
Table 4
Constraints for SPEKE and DH-EKE
4.1
Discrete log attack
4.2 Leaking
information
4.2.1
DH-EKE partition attack
4.2.2
SPEKE partition attack |
4.3
Subgroup confinement
Figure 4.3
Subgroups of Zp* for a safe prime p = 2q+1
4.4
Omitting encryption in DH-EKE
4.5 Using a
short modulus
4.6
Uncertified ephemeral parameters
Table 4.6
Special constraints for chosen parameters
4.6.1 A
user-to-station protocol
4.7 Using a
short exponent
4.8 More
desirable characteristics
4.9 Stolen
session key attack
4.10
Verification stage attacks
4.11
Detecting on-line attack
4.12 The
"password in exponent" attack
4.13
Choosing f(s)
4.14
Application to Kerberos
- A
fully constrained SPEKE
- Other limitations and
possibilities
Need for a trusted
path
Formal verification
- Other related
work
- Uses of password-only
authenticated exchange
- Summary
- References
- Appendix A
Group theory relevant to Diffie-Hellman methods
Copyright © 1996-1997 Integrity Sciences, Inc. All rights reserved.
